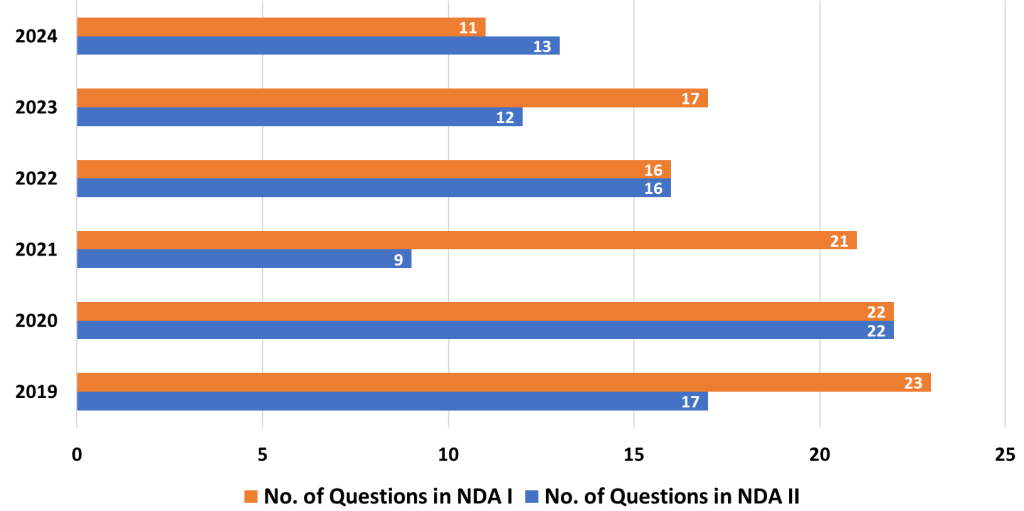
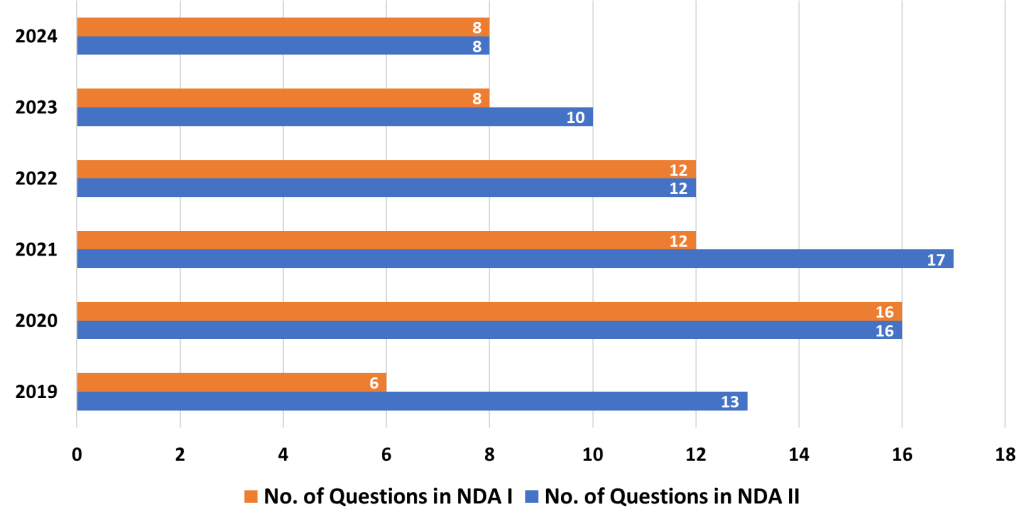
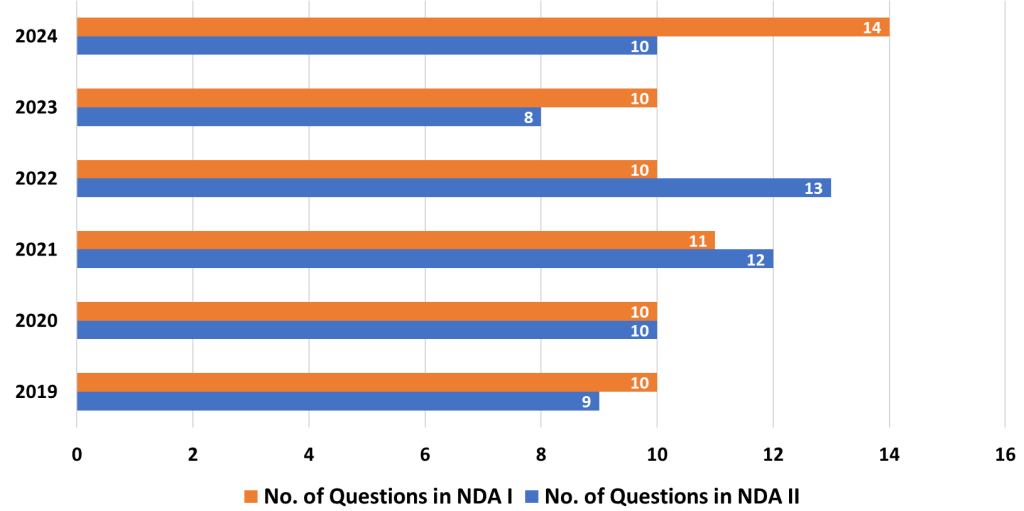
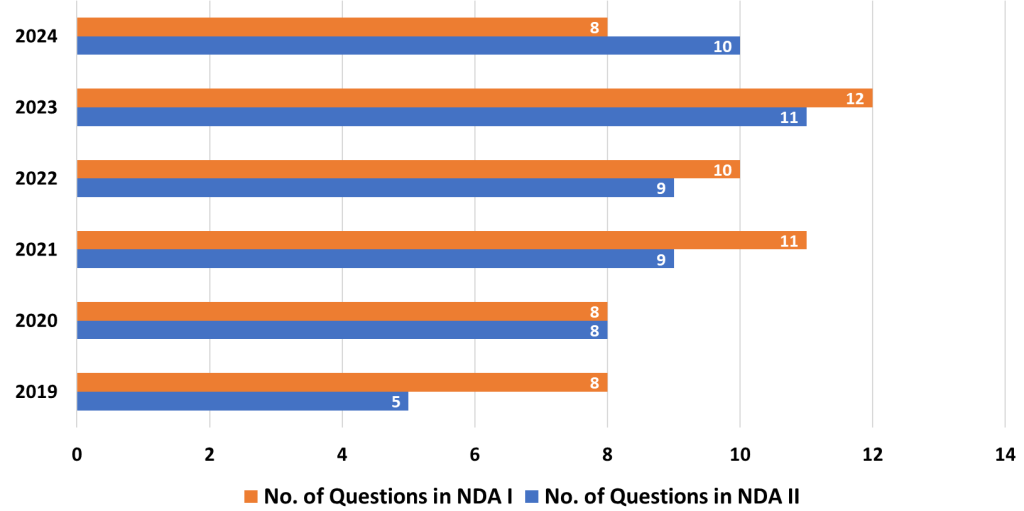
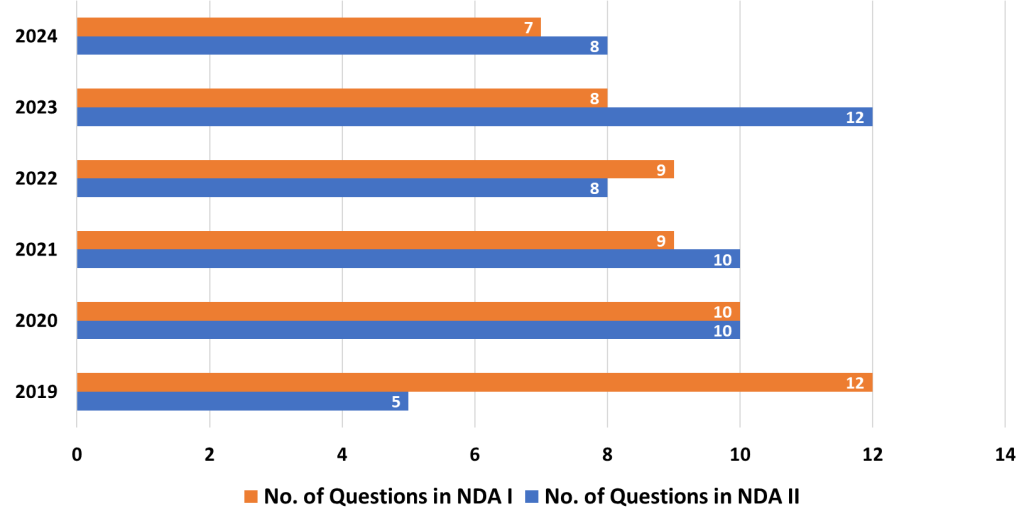
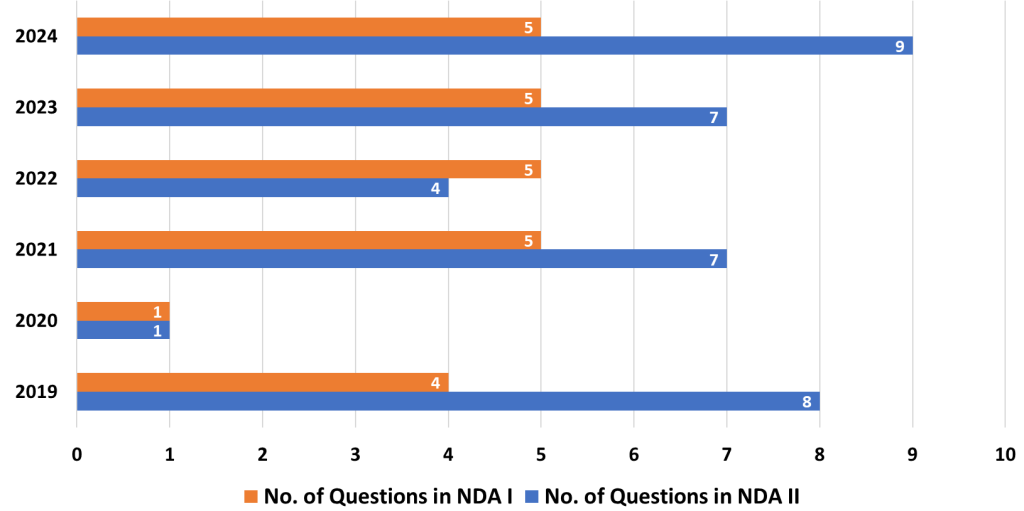
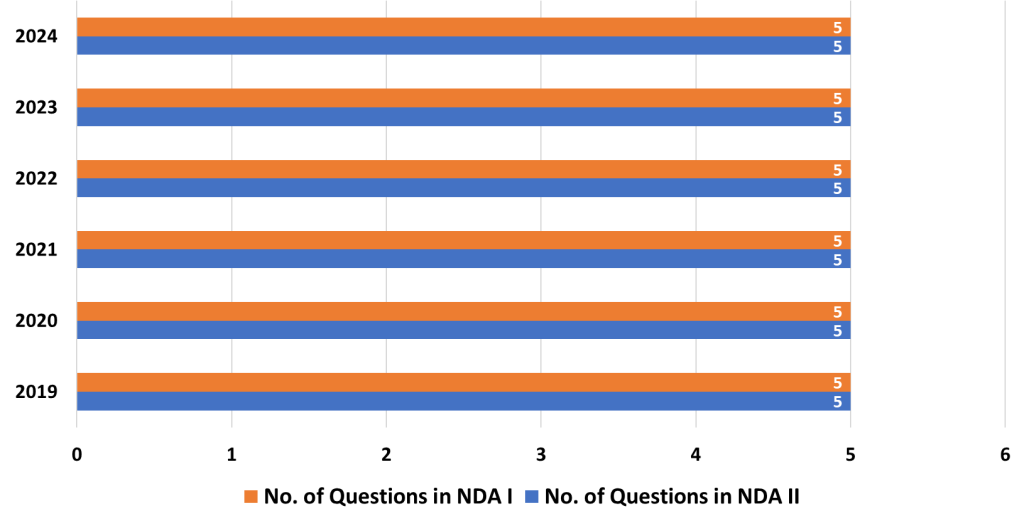
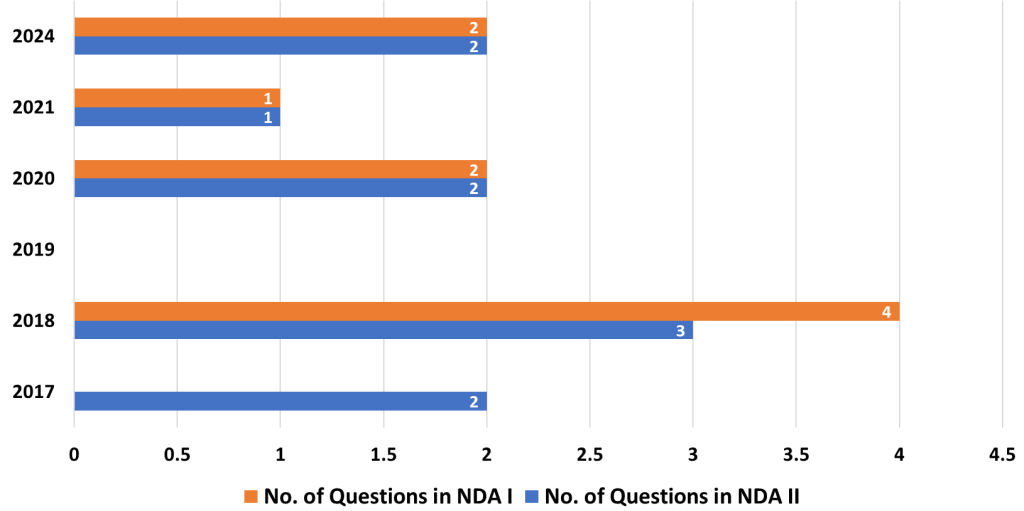
The Mathematics Paper in the National Defence Academy and Naval Academy (NDA-NA) exam is a crucial component for candidates aspiring to join these prestigious institutions. It requires a solid understanding of various mathematical concepts, both foundational and advanced. Here’s an in-depth analysis of the topics based on their importance, along with strategies to help you prepare effectively for the exam.
Most Important Topics
1. Trigonometry
- Analysis: Trigonometry plays a key role in the NDA-NA exam, with frequent questions revolving around trigonometric identities, ratios, and angle calculations. Trigonometric functions are used to solve problems related to heights, distances, and circular motion, making it essential for both theoretical and application-based questions.
- Strategy: Build a strong conceptual foundation of trigonometric functions and their relationships. Focus on mastering the properties and identities. Practice applying trigonometric principles to real-world problems, such as solving for unknown angles or distances. Regular revision and problem-solving practice will help solidify your understanding.
2. Differential Calculus
- Analysis: Differential Calculus tests your understanding of how quantities change. Problems often involve finding rates of change, tangents, and solving for maximum or minimum values. It is a vital topic because its concepts appear in various applications, including physics and engineering problems.
- Strategy: Focus on understanding the concept of derivatives and their practical uses. Practice solving problems involving rate changes, tangent lines, and optimization. Learn to approach questions systematically by identifying key variables and relationships between them.
3. Integral Calculus
- Analysis: Integral Calculus is essential for calculating areas, volumes, and understanding accumulation. It is often combined with geometry to solve problems that require determining the area under curves or between curves.
- Strategy: Build a strong understanding of integration techniques and their applications. Practice problems that involve calculating areas and volumes. Visualizing problems geometrically can be a great aid in solving them efficiently.
4. Probability
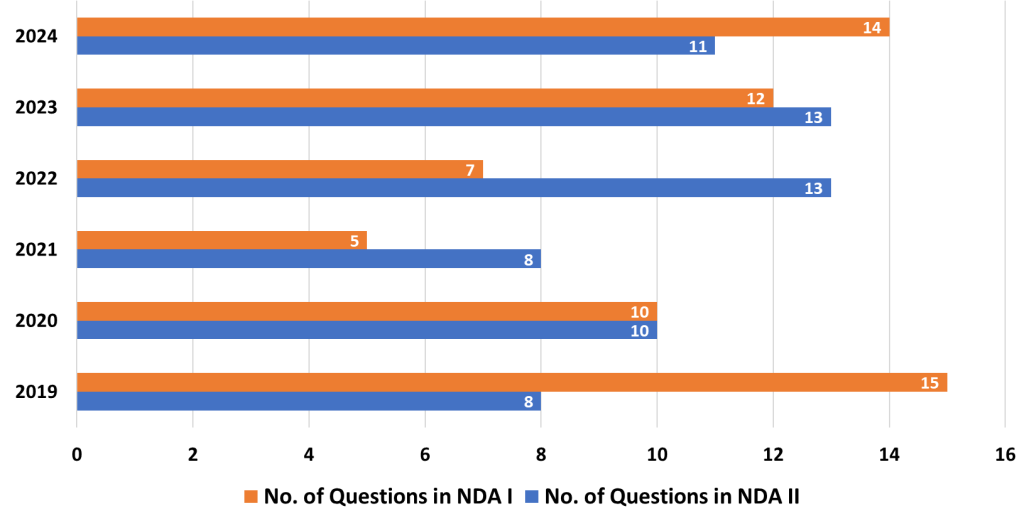
- Analysis: Probability questions test your understanding of the likelihood of events occurring. This topic involves theoretical probability, combinatorics, and real-world applications, such as drawing cards or tossing dice.
- Strategy: Focus on learning the basics of probability theory and applying them to practical problems. Practice different types of probability questions, including those involving multiple events. Understanding permutations and combinations will also help solve these problems more effectively.
5. Statistics
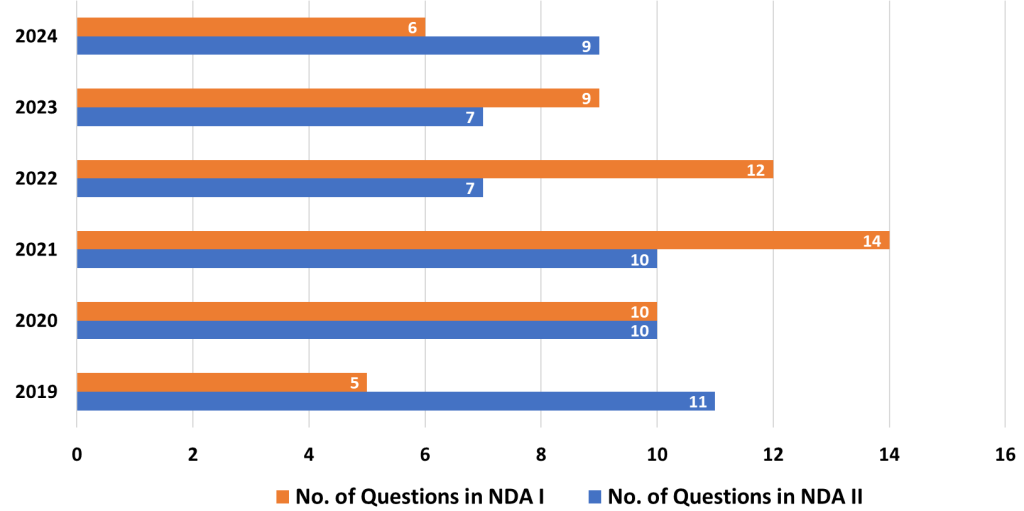
- Analysis: Statistics involves understanding data, its distribution, and measures of central tendency (mean, median, mode). Questions in this topic require interpreting data and making predictions based on given information.
- Strategy: Strengthen your ability to interpret and analyze data. Practice calculating averages, understanding data spread, and identifying trends. Graph interpretation and the ability to summarize data concisely are crucial.
6. Matrices and Determinants
- Analysis: Matrices and Determinants are integral in solving systems of linear equations and performing operations such as finding inverses and solving simultaneous equations. This topic frequently appears due to its practical applications in vector spaces and transformations.
- Strategy: Learn the operations on matrices, such as addition, multiplication, and finding determinants. Practice solving systems of equations using matrices, as these are common in the NDA-NA exam. Visualize how matrices transform data, especially in geometric contexts.
7. Analytical Geometry 2D
- Analysis: Analytical Geometry deals with the geometry of shapes using coordinate systems. It includes questions on lines, circles, parabolas, ellipses, and hyperbolas. This topic combines geometry with algebra and is crucial for spatial reasoning.
- Strategy: Focus on visualizing shapes in the coordinate plane. Practice finding equations of lines, angles, and distances between points. Be comfortable working with different conic sections and understand their properties in both algebraic and geometric contexts.
Medium Weightage Topics
8. Sets, Relations and Functions
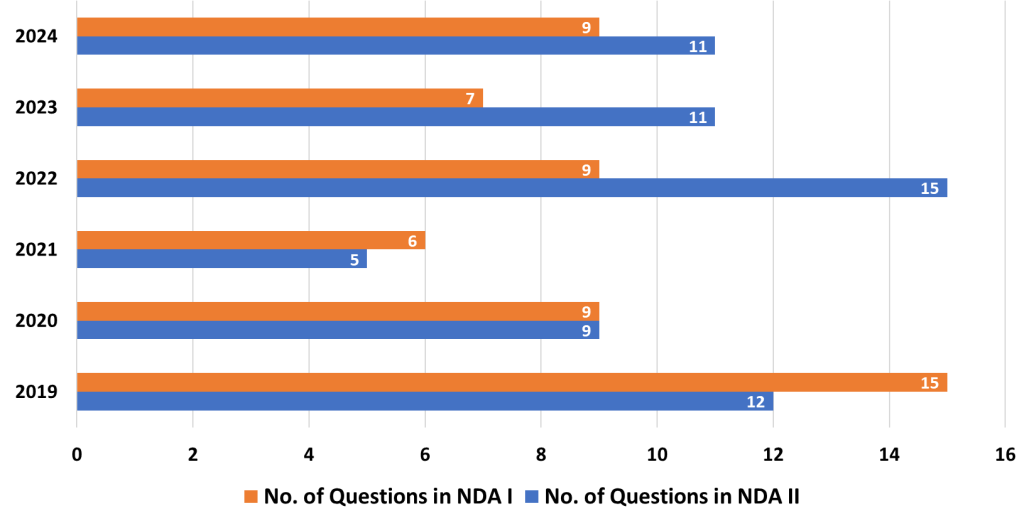
- Analysis: Functions explore the relationships between variables. The NDA-NA exam tests understanding of different types of functions, such as linear, quadratic, exponential, and logarithmic functions, as well as their properties.
- Strategy: Build familiarity with function notation and be able to analyze and interpret graphs. Practice transforming functions and solving word problems that describe functional relationships. Understanding inverse functions and composition of functions is also critical.
9. Sequence and Series
- Analysis: Sequence and Series focus on the progression of numbers in patterns, such as arithmetic and geometric progressions. Questions may involve finding specific terms in a sequence or the sum of a series.
- Strategy: Understand how to identify and analyze patterns in sequences. Practice solving problems related to the sum of terms in both arithmetic and geometric progressions. Pay attention to real-world applications, such as compound interest, which often involves sequences and series.
10. Vector Algebra
- Analysis: Vector Algebra deals with quantities that have both magnitude and direction. It includes operations such as addition, subtraction, and scalar multiplication of vectors. Vectors are commonly applied in physics-related questions, especially in mechanics and motion.
- Strategy: Focus on understanding the geometric representation of vectors. Practice solving problems involving vector addition, dot products, and cross products. Visualization is key to mastering this topic, as vectors require a strong understanding of spatial relationships.
11. Quadratic Equations and Inequalities
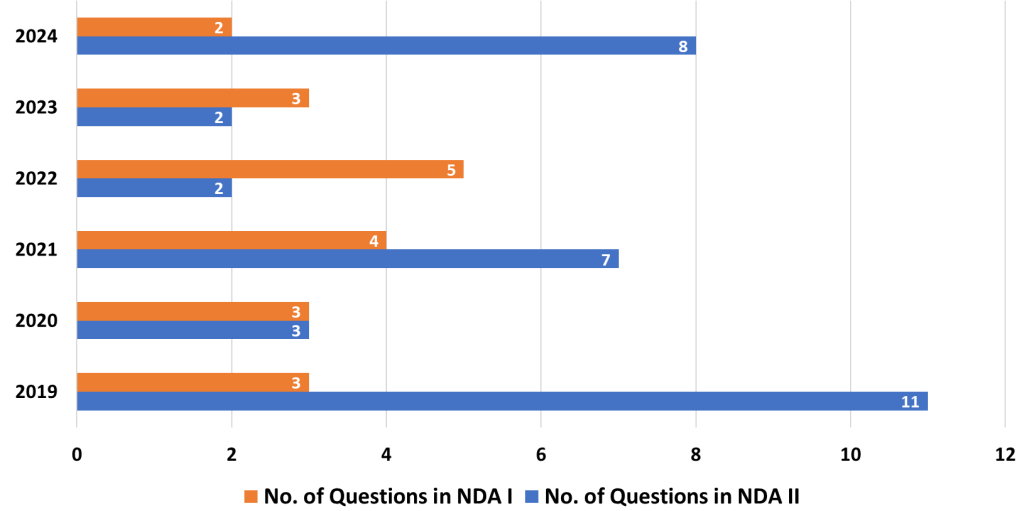
- Analysis: Quadratic equations frequently appear in the NDA-NA exam, with questions focusing on solving these equations and understanding their real-world applications. Quadratics also form the basis for more complex topics like optimization and motion problems.
- Strategy: Practice solving quadratic equations using various methods such as factorization, completing the square, and the quadratic formula. Understand the relationships between the coefficients and the roots, as well as the geometric interpretation of these equations.
12. Permutations and Combinations
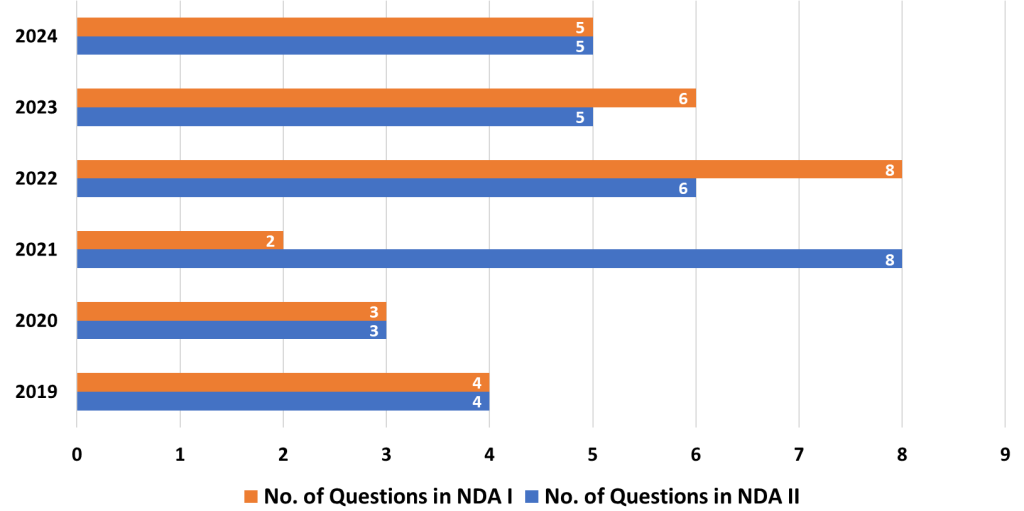
- Analysis: Permutations and Combinations are essential for solving problems related to counting and probability. These concepts are used to determine the number of ways objects can be arranged or selected.
- Strategy: Strengthen your ability to distinguish between permutations (where order matters) and combinations (where order doesn’t matter). Practice solving a wide variety of problems related to counting arrangements, selections, and probability.
Least Weightage Topics
13. Logarithms
- Analysis: Logarithms are not heavily emphasized in the NDA-NA exam but may appear in questions related to simplifying expressions or solving equations. Understanding logarithmic relationships can also be useful in solving problems involving exponential growth.
- Strategy: Focus on the properties of logarithms and practice simplifying expressions that involve them. Understand their relationship to exponents, as this will help in solving word problems and equations efficiently.
14. Binary Numbers
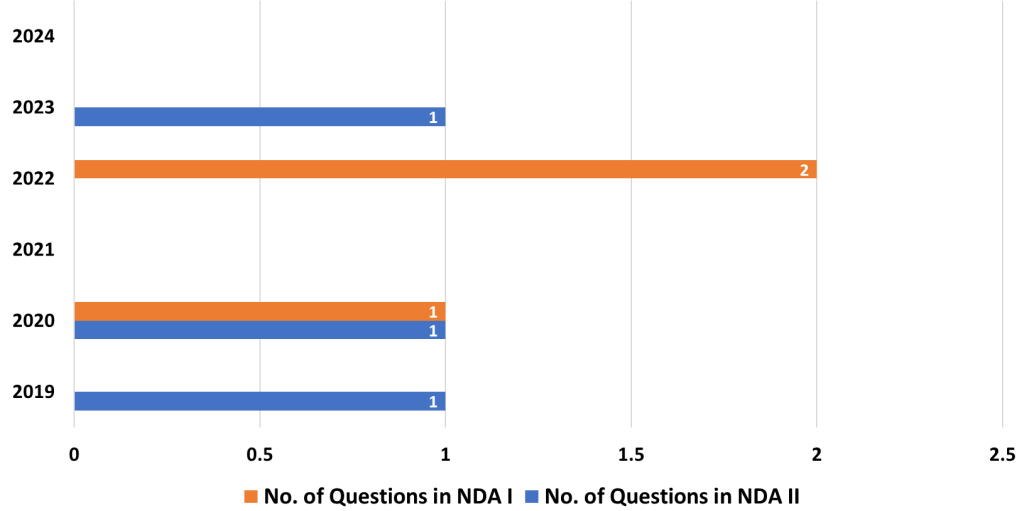
- Analysis: Binary numbers appear less frequently in the NDA-NA exam, but they are crucial for understanding digital systems and coding. These questions often involve converting numbers between binary and decimal systems.
- Strategy: Practice converting numbers between binary, decimal, and other numeral systems. Focus on understanding how binary operations work, especially in terms of logic gates and circuits.
15. Binomial Theorem
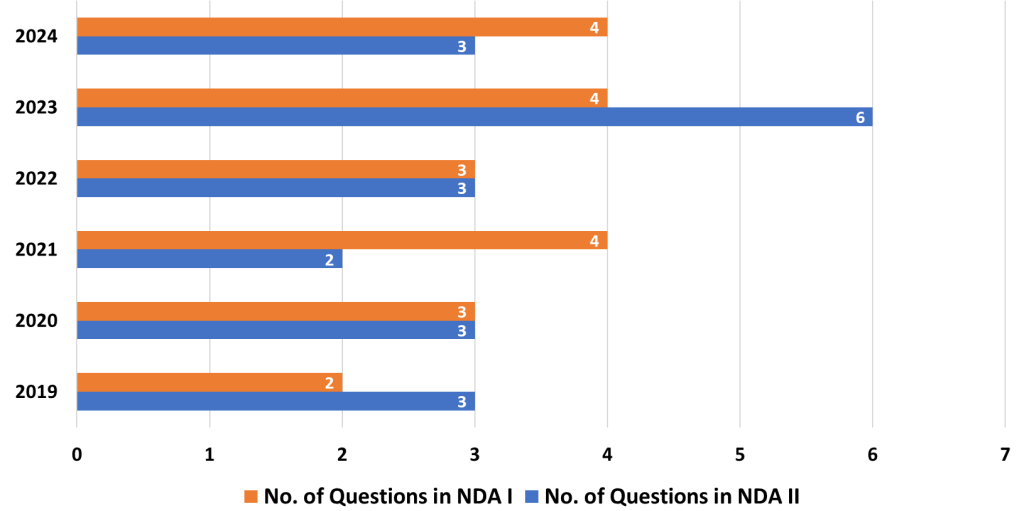
- Analysis: The Binomial Theorem allows for the expansion of powers of binomials. This topic doesn’t carry heavy weight in the exam but can be tested occasionally in algebra-related problems.
- Strategy: Understand the concept of binomial expansion and how it applies to algebraic expressions. Practice applying the theorem to various problems involving large powers, which can be solved more easily using this method.
General Preparation Strategies for NDA-NA Mathematics Paper
- Understand the Exam Pattern: Knowing the relative weightage of topics is essential for efficient preparation. Focus on the most important topics such as Trigonometry, Calculus, and Probability while ensuring that you’re also prepared for medium and least weightage topics.
- Master the Basics: A strong understanding of basic mathematical concepts is critical. Make sure to review key principles and foundational topics, as they will be essential for solving more advanced problems.
- Practice Regularly: Consistent practice is key to success in the NDA-NA exam. Solve mock tests, sample papers, and previous years’ question papers to familiarize yourself with the question format and difficulty level.
- Focus on Time Management: Time management is crucial during both preparation and the actual exam. While practicing, try to solve questions under timed conditions to improve your speed and accuracy.
- Use Shortcuts and Tricks: Once you are confident in your basic knowledge, learn and apply shortcuts for solving problems faster. This is especially useful in topics like Trigonometry and Calculus, where lengthy calculations can be simplified using tricks.
- Revise Regularly: Ensure that you revisit and revise all topics periodically. This helps retain concepts and ensures that you can recall them quickly during the exam.
- Clear Doubts Immediately: If you encounter a difficult concept, clarify it immediately. Don’t let doubts linger, as they can slow down your progress in solving related questions.
By following these strategies and focusing on key topics, candidates can improve their chances of performing well in the NDA-NA Mathematics Paper. Consistent effort, a clear understanding of concepts, and efficient problem-solving skills will lead to success in the exam.