If you are an aspirant of CDS Entry for IMA then you have to write mathematics exam paper along with english and General Knowledge. As per the CDS Exam pattern appearing candidates have to attempt 100 questions in 120 minutes, that just means, you not just have to find the solution of a problem but you have to solve it in less than a minute. CDS Maths exam is all about quick recognition-quick logic-quick application, a candidates has to recognise or understand the problem as he/she reads it and remember the logic or formula or method to solve it and quickly apply it to find the answer from the given choices. In this article we are sharing 10 problems and expect our interested readers to solve them within 10 minutes and share the answer in the comments.

10 Minutes 10 Numerical’s – Challenge for CDS IMA Aspirants

Given numerical’s belongs to the category of more often asked types of questions that are expected in CDS Exam.

• The compound interest for two years on a capital is Rs. two more than the simple interest for the same period.  If the rate of interest is 5% per year, then the capital would be

(a) Rs. 800

(b) Rs. 840

(c) Rs. 880

(d) Rs. 882

• If Rs. 370 are divided among 10 men, 12 women and 20 boys such that each man gets an amount equal to that received by one woman and one boy together and that each woman gets twice the amount received by a boy, then the amount received by 10 men would be

(a) Rs. 100

(b) Rs. 150

(c) Rs. 120

(d) Rs. 130

• If two numbers are in the ratio of 2 : 3 and the product of their HCF and LCM is 33750, then the sum of the numbers is

(a) 250

(b) 425

(c) 325

(d) 375

• xy (z² + 1) + z(x² + y²) can be factorised as

(a) (xy + z) (yz + x)

(b) (zx + y) (xy + z)

(c) (yz + x) )(zx + y)

(d) (x² + y²) (z + x)

• For any three sets, A, B and C, A ∩ (B ∪ C) is equal to

(a) (A ∪ C) ∩ (B ∪ C)

(b) (A ∩ B) ∪ (A ∩ C)

(c) (A∪B) ∩ C

(d) (A ∩ B) ∪ C

• The cost price of a table and a chair together is Rs. 430. If the table costs 15% more than the chair, then the cost (in rupees) of the table and the chair are respectively

(a) 196 and 175

(b) 230 and 200

(c) 200 and 170

(d) 240 and 190

• If the slope of one of the lines x² – 4xy + y² = 0 is k times the slope of the other, then the value of k is equal to

(a) 3± √7

(b) 7± 2√3

(c) 7± 4√3

(d) 3± 2√3

• In the given figure, AB = 6 cm and O is the middle point of AB. Semicircles are drawn on AB, AO and OB. If C is the centre of the small circle which touches all the semi-circles, then the radius of this small circle is

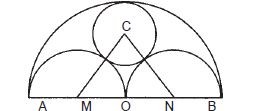
(a) 3 cm

(b) 2.25 cm

(c) 1 cm

(d) 2 cm

• Solid spherical balls each of diameter 1.4 cm are dropped into a cylindrical beaker containing water upto a height of 28 cm and are fully submerged. The diameter of the beaker is 5.6 cm. If the water in the beaker rises by 17.5 cm, then the number of balls dropped in it will be

(a) 63

(b) 100

(c) 300

(d) 780

• A flag-staff is fixed at the top of a tower. The angles of elevation of the top and the bottom of this flag staff at a point distant ‘a’ metres from the foot of the tower are α and β respectively. The height of the flag-staff (in metres) is

(a) a (sin α – sin β)

(b) a (cos β – cos α)

(c) a (tan α – tan β)

(d) a tan (α – β)

If you find it hard to solve these problems in less than 10 minutes then you need to pace up your solving skills, and you can do it only by regular scheduled practice. We can help you in increasing your solving speed by giving you a proper platform to practice your solving skills of CDS exam MCQs. Join our customised test series and practice your skills with our advanced analysis tools, TO KNOW MORE CLICK ON LINK GIVEN BELOW.

CDS 2 2016 Exam Online Coaching