NDA 2 2017 Written Mathematics Exam Formulas

NDA written exam is conducted by UPSC (Union Public Service Commission) twice every year. Candidates should know about the syllabus of the NDA written exam in the process of NDA exam preparation. In this article we will see NDA 2 2017 Written Mathematics Exam Formulas.

NDA 2 2017 Written Mathematics Exam Formulas

• Set Theory is a branch of mathematics which deals with the study of sets or the collection of similar objects.
• Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both. The union of{1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4} .
• Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B. The intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3} .
• Set difference of U and A, denoted U \ A, is the set of all members of U that are not members of A. The set difference{1,2,3} \ {2,3,4} is {1} , while, conversely, the set difference {2,3,4} \ {1,2,3} is {4} . When A is a subset of U, the set difference U \ A is also called the complement of A in U. In this case, if the choice of U is clear from the context, the notation Ac is sometimes used instead of U \ A, particularly if U is a universal set as in the study of Venn diagrams.
• Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1,2,3} and {2,3,4} , the symmetric difference set is {1,4} . It is the set difference of the union and the intersection, (A ∪ B) \ (A ∩ B) or(A \ B) ∪ (B \ A).
• Cartesian product of A and B, denoted A × B, is the set whose members are all possible ordered pairs (a,b) where ais a member of A and b is a member of B. The cartesian product of{1, 2} and {red, white} is {(1, red), (1, white), (2, red), (2, white)}.
• Power set of a set A is the set whose members are all possible subsets of A. For example, the power set of {1, 2} is{ {}, {1}, {2}, {1,2} } .
• Set Theory Formulas (Notations): 

• De Morgan’s laws: De Morgan’s laws are a pair of transformation rules relating the set operators “union” and “intersection” in terms of each other by means of negation.

1. Demorgan’s First Law: (A ∪ B)’ = (A)’ ∩ (B)’

The first law states that the complement of the union of two sets is the intersection of the complements

2. Demorgan’s Second Law: (A ∩ B)’ = (A)’ ∪ (B)’

The second law states that the complement of the intersection of two sets is the union of the complements.

• Cartesian product and relation:

1. Cartesian product: If A and B are sets, the Cartesian product of A and B is the set

A × B = {(a, b):(a ∈ A) and (b ∈ B)}.

The following points are worth special attention: The Cartesian product of two sets is a set, and the elements of that set are ordered pairs. In each ordered pair, the first component is an element of A, and the second component is an element of B.

2. Relation: A relation from a set A to a set B is a subset of A×B. A (binary) relation on A is a subset of A × A.
3. Equivalence relation: A given binary relation ‘~’ on a set X is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive. Equivalently, for all a, b and c in X: a ~ a. (Reflexivity); if a ~ b then b ~ a. (Symmetry); if a ~ b and b ~ c then a ~ c. (Transitivity)

• Representation of real numbers on a line: Real numbers (R): Every number, which is either rational or irrational, is called a real number. In other words, a set of real numbers is the union of set of rational numbers and set of irrational numbers. Rational numbers: Any number which can be expressed in the form of a/b, where a and b both are integers and b is not equal to zero, is a rational number. Irrational numbers: The numbers which are not rational, are called irrational numbers.

A real number line is a familiar way to picture various sets of numbers. For example, the divisions marked on a number line show the integers, which are the counting numbers {1, 2, 3,…}, with their opposites {−1, −2, −3,…}, with the number 0, which divides the positive numbers on the line from the negative numbers.

• Complex number: A complex number is made up of both real and imaginary components. It can be represented by an expression of the form (a+bi), where a and b are real numbers and i is imaginary. When defining i we say that i = . Then we can think of i² as -1.

1. Commutativity z₁ + z₂ = z₂ + z₁, z₁z₂ = z₂z₁
2. Associativity z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃, z₁(z₂z₃) = (z₁z₂)z₃
3. Distributivity z₁(z₂ + z₃) = z₁z₂ + z₁z₃
4. Additive and Multiplicative Identities 0 + z = z, 1.z = z
5. Modulus and Argument of a complex number: modulus and argument of a complex number are the quantities which can be recognised by looking at an Argand diagram. Any complex number, z, can be represented by a point in the complex plane as shown 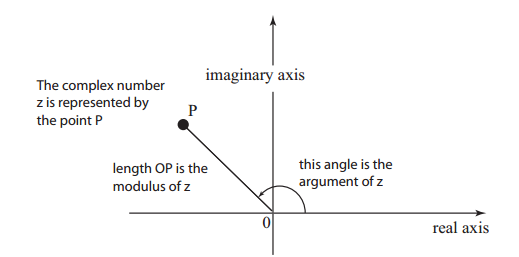The complex number z is represented by point P. We can join point P to the origin with a line segment, as shown. We associate with this line segment two important quantities. The length of the line segment, that is OP, is called the modulus of the complex number. The angle from the positive axis to the line segment is called the argument of the complex number, z.

• Conversion of a number in decimal system to binary system: Decimal number system is the most commonly used and the most familiar one to the general public. It is also known as Base 10 numbering system since it is based on 10 following symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Binary is the simplest kind of number system that uses only two digits of 0 and 1. The following technique, called the (Division – Remainder Technique) is easiest & simple method used to convert decimal to binary numbers:

1. Step : Divide the decimal number to be converted by the value of the new base. In this case divide it by 2.
2. Step : Record the remainder from Step – 1 as the rightmost digit.
3. Step : Divide the quotient of the previous by the new base.
4. Step : Record the remainder from Step – 3 as the next digit (to the left) of the new base number.
5. Step : Bottom to top sequence of remainder will be the required converted number. Repeat Step 3 and Step 4, recording remainders from right to left, until the quotient becomes less than the digit of new base so that it cannot be divided.