The Numerical Ability section of the Air Force Common Admission Test (AFCAT) evaluates candidates’ aptitude in fundamental mathematical principles, including arithmetic, algebra, and applied problems. This section typically comprises 15 to 20 questions, emphasizing speed and accuracy. Proficiency in core formulas enables efficient resolution of these questions within the allotted time. The following compilation organizes essential formulas by topic, drawing from standard preparation resources. Each formula is accompanied by a brief explanation to facilitate understanding and application.
You must have a proper strategy to boost the score in exam. Candidates must refer to the previous years’ question papers and mock tests. They should also check the syllabus and exam pattern to know more details about the topics and exam structure. Here, we are providing with AFCAT-Numerical ability- Most important formulas that will help candidates to quickly recall for their last-minute revision to not miss any single question based upon formula in Numerical ability section of AFCAT written examination.
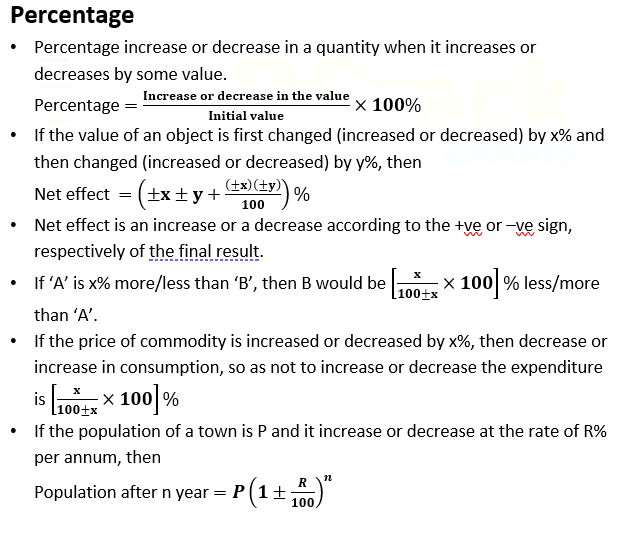
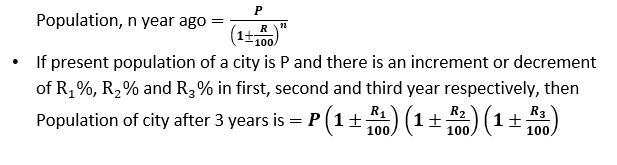



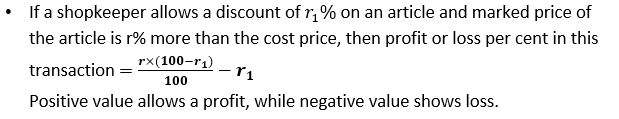








Speed, Distance, and Time
This topic involves calculations related to motion, relative speeds, and conversions. Key formulas include:
- Unit Conversion: Speed in m/s = Speed in km/h × (5/18) Speed in km/h = Speed in m/s × (18/5)
- Average Speed: For distances covered at speeds x km/h for t hours and y km/h for T hours: ( (x × t + y × T) / (t + T) ) For two equal distances at speeds x and y km/h: (2xy) / (x + y)
- Relative Speed: Objects moving in opposite directions: x + y km/h Objects moving in the same direction: x – y km/h
- Late/Early Arrival: If speed changes to (x/ y) of usual and results in t minutes late: Usual time = (t × y) / (x – y) Distance when late by t hours at x km/h and early by T hours at y km/h: (xy (t + T)) / (y – x)
- Trains: Time to cross a stationary object of length y m (train length x m): Time to cover (x + y) m Time to cross another train of length L m at speed S m/s: (l + L) / (s ± S)
- Boats and Streams: Downstream speed: Boat speed (x) + Stream speed (y) Upstream speed: x – y Speed in still water: (1/2) × (Upstream + Downstream)
- Races: If A beats B by x m in a d m race: Speed ratio A:B = d : (d – x)
Work and Time
Focuses on work rates, efficiency, and combined efforts, often applied to pipes and cisterns.
- Work Rate: Work done by A in D days: 1 day’s work = 1/D Work in t days: t / D
- Combined Work: A and B together (A in x days, B in y days): (xy) / (x + y) days For three pairs (A+B in x, B+C in y, C+A in z): (2 xyz) / (xy + yz + zx) days
- Efficiency: If A is x times as efficient as B: Work ratio = x : 1; Time ratio = 1 : x
- Pipes and Cisterns: Fill rate for a pipe filling in x hours: 1/x per hour Combined rate for two pipes: 1/x + 1/y
Percentage
Essential for calculations involving proportions, increases, and decreases.
- Basic Conversion: a% = a/100 Fraction to percentage: (a/b) × 100%
- Increase/Decrease: Percentage change = (Change / Initial value) × 100% If A is x% more than B: B is (x / (100 + x)) × 100% less than A
- Net Effect: After +x% and +y%: x + y + (xy)/100 After +x% and –y%: x – y – (xy)/100
- Population/Depreciation: After n years at R%: P × (1 ± R/100)^ n
Average
Used for central tendency in data sets.
- General Average: Sum of values / Number of values
- Specific Averages: First n natural numbers: (n + 1)/2 First n even numbers: n + 1 First n odd numbers: n Squares of first n naturals: (n + 1)(2n + 1)/6 Cubes of first n naturals: [n(n + 1)/2]^2
Simple and Compound Interest
Covers financial growth over time.
- Simple Interest (SI): SI = (P × R × n)/100 Rate for sum becoming n times in T years: R = 100(n – 1)/T %
- Compound Interest (CI): Amount = P × (1 + R/100)^ n CI = Amount – P Half-yearly: P × (1 + R/200)^ (2n) Quarterly: P × (1 + R/400)^ (4n)
- SI vs. CI Difference: For 2 years: P × (R/100) × (2R + 100)/100 For 3 years: P × (R/100) × (3R^2 + 300R + 30,000)/10,000
Ratio and Proportion
Deals with comparisons and mixtures.
- Types of Ratios: Compound: Product of ratios Duplicate: Square of ratio Reciprocal: 1/a : 1/b
- Mixtures/Alligation: Ratio of quantities = (Price2 – Mean) : (Mean – Price1)
Profit and Loss
Focuses on commercial arithmetic.
- Basic: Gain = SP – CP Gain % = (Gain / CP) × 100% SP = CP × (1 + Gain%/100) CP = SP × (100 / (100 + Gain%))
- Equal Percentages: If sold at +x% and –x%: Loss % = (x/10)^2 %
Decimal Fractions and Simplification
Involves order of operations and algebraic identities.
- BODMAS Rule: Brackets, Of, Division, Multiplication, Addition, Subtraction
- Algebraic Identities: (a + b)(a – b) = a^2 – b^2 (a + b)^2 = a^2 + 2a**b + b^2 (a – b)^2 = a^2 – 2a**b + b^2 a^3 + b^3 = (a + b)(a^2 – a**b + b^2) a^3 – b^3 = (a – b)(a^2 + a**b + b^2) If a + b + c = 0, then a^3 + b^3 + c^3 = 3abc
These formulas represent the core elements frequently tested in AFCAT. Candidates are advised to practice application through solved examples and mock tests to enhance speed and precision. For further details, consult official AFCAT guidelines and reputable preparation materials.







