Maths Formulas Used in NDA Exam: The National Defence Academy (NDA) examination is an entrance exam in India for those aspiring to join the Indian Armed Forces. The NDA exam comprises various subjects, and Mathematics is a significant component.
Here’s a list of some common mathematical formulas and concepts often tested in the NDA exam:
- Algebra:
- Quadratic Equations
- Arithmetic and Geometric Progressions
- Binomial Theorem for positive integral indices
- Trigonometry:
- Basic identities
- Trigonometric ratios and their relations
- Compound angles formulas, Multiple & Sub-multiple angles formulas
- Solution of trigonometric equations
- Matrices and Determinants:
- Types of matrices, operations, and their properties
- Determinant properties and finding the inverse of a matrix using determinants
- Differential Calculus:
- Concept of a function, domain, and range
- Derivative and its geometrical and physical interpretations
- Applications of derivatives: Rate of change, Tangents & Normals, Maxima & Minima
- Integral Calculus:
- Integration as the inverse process of differentiation
- Basic integrals of standard functions
- Definite integrals and their properties
- Application of Integrals: Area under simple curves
- Differential Equations:
- Order and degree of a differential equation
- Solutions of differential equations by various methods
- Vector Algebra:
- Vectors and their properties
- Scalar and vector products of two vectors
- Statistics and Probability:
- Measures of Central Tendency and Variability
- Permutations and Combinations:
- Probability concepts and Bayes’ theorem
- Analytical Geometry of Two and Three Dimensions:
- Distance formula, section formula
- Equation of a line, plane, sphere
- Angle between two lines, a line and a plane
- Numbers and Basic Number Systems:
- Prime numbers, Factors, and Multiples
- Basic properties of numbers and their operations
- Complex Numbers:
- Basic operations, polar representation, and De Moivre’s theorem
This list is not exhaustive, but it does cover many of the primary mathematical concepts tested in the NDA exam. It’s essential to get a detailed syllabus and go through textbooks or preparatory guides to ensure comprehensive preparation.
NDA Paper 1 Mathematics syllabus:
- Algebra
Concept of a set, operations on sets, Venn diagrams, De Morgan laws, Cartesian product, relation, equivalence relation, Representation of real numbers on a line, Complex numbers – basic properties, modulus, argument, cube roots of unity, Binary system of numbers, Conversion of a number in decimal system to binary system and vice-versa, Arithmetic, Geometric and Harmonic progressions. Quadratic equations with real coefficients, Solution of linear inequations of two variables by graphs, Permutation and Combination, Binomial theorem and its applications, Logarithms and their applications.
- Matrices and Determinants
- Trigonometry
- Analytical Geometry – 2D and 3D
- Differential Calculus
- Integral calculus and Differential equations
- Vector algebra
- Statistics and Probability
Common Formulas Used in NDA Exam
- Set Theory is a branch of mathematics which deals with the study of sets or the collection of similar objects.
- Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both. The union of{1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4} .
- Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B. The intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3} .
- Set difference of U and A, denoted U \ A, is the set of all members of U that are not members of A. The set difference{1,2,3} \ {2,3,4} is {1} , while, conversely, the set difference {2,3,4} \ {1,2,3} is {4} . When A is a subset of U, the set difference U \ A is also called the complement of A in U. In this case, if the choice of U is clear from the context, the notation Ac is sometimes used instead of U \ A, particularly if U is a universal set as in the study of Venn diagrams.
- Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1,2,3} and {2,3,4} , the symmetric difference set is {1,4} . It is the set difference of the union and the intersection, (A ∪ B) \ (A ∩ B) or(A \ B) ∪ (B \ A).
- Cartesian product of A and B, denoted A × B, is the set whose members are all possible ordered pairs (a,b) where ais a member of A and b is a member of B. The cartesian product of{1, 2} and {red, white} is {(1, red), (1, white), (2, red), (2, white)}.
- Power set of a set A is the set whose members are all possible subsets of A. For example, the power set of {1, 2} is{ {}, {1}, {2}, {1,2} } .
- Set Theory Formulas (Notations):
- For a group of two sets:
- De Morgan’s laws: De Morgan’s laws are a pair of transformation rules relating the set operators “union” and “intersection” in terms of each other by means of negation.
- Demorgan’s First Law: (A ∪ B)’ = (A)’ ∩ (B)’
The first law states that the complement of the union of two sets is the intersection of the complements
- Demorgan’s Second Law: (A ∩ B)’ = (A)’ ∪ (B)’
The second law states that the complement of the intersection of two sets is the union of the complements.
- Cartesian product and relation:
- Cartesian product: If A and B are sets, the Cartesian product of A and B is the set
A × B = {(a, b):(a ∈ A) and (b ∈ B)}.
The following points are worth special attention: The Cartesian product of two sets is a set, and the elements of that set are ordered pairs. In each ordered pair, the first component is an element of A, and the second component is an element of B.
- Relation: A relation from a set A to a set B is a subset of A×B. A (binary) relation on A is a subset of A × A.
- Equivalence relation: A given binary relation ‘~’ on a set X is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive. Equivalently, for all a, b and c in X: a ~ a. (Reflexivity); if a ~ b then b ~ a. (Symmetry); if a ~ b and b ~ c then a ~ c. (Transitivity)
- Representation of real numbers on a line: Real numbers (R): Every number, which is either rational or irrational, is called a real number. In other words, a set of real numbers is the union of set of rational numbers and set of irrational numbers. Rational numbers: Any number which can be expressed in the form of a/b, where a and b both are integers and b is not equal to zero, is a rational number. Irrational numbers: The numbers which are not rational, are called irrational numbers.
A real number line is a familiar way to picture various sets of numbers. For example, the divisions marked on a number line show the integers, which are the counting numbers {1, 2, 3,…}, with their opposites {−1, −2, −3,…}, with the number 0, which divides the positive numbers on the line from the negative numbers.
- Complex number: A complex number is made up of both real and imaginary components. It can be represented by an expression of the form (a+bi), where a and b are real numbers and i is imaginary. When defining i we say that i =
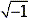 . Then we can think of i2 as -1.
. Then we can think of i2 as -1.
- Commutativity z1 + z2 = z2 + z1, z1z2 = z2z1
- Associativity z1 + (z2 + z3) = (z1 + z2) + z3, z1(z2z3) = (z1z2)z3
- Distributivity z1(z2 + z3) = z1z2 + z1z3
- Additive and Multiplicative Identities 0 + z = z, 1.z = z
- Modulus and Argument of a complex number: modulus and argument of a complex number are the quantities which can be recognised by looking at an Argand diagram. Any complex number, z, can be represented by a point in the complex plane as shown The complex number z is represented by point P. We can join point P to the origin with a line segment, as shown. We associate with this line segment two important quantities. The length of the line segment, that is OP, is called the modulus of the complex number. The angle from the positive axis to the line segment is called the argument of the complex number, z.
- Conversion of a number in decimal system to binary system: Decimal number system is the most commonly used and the most familiar one to the general public. It is also known as Base 10 numbering system since it is based on 10 following symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Binary is the simplest kind of number system that uses only two digits of 0 and 1. The following technique, called the (Division – Remainder Technique) is easiest & simple method used to convert decimal to binarynumbers:
- Step : Divide the decimal number to be converted by the value of the new base. In this case divide it by 2.
- Step : Record the remainder from Step – 1 as the rightmost digit.
- Step : Divide the quotient of the previous by the new base.
- Step : Record the remainder from Step – 3 as the next digit (to the left) of the new base number.
- Step : Bottom to top sequence of remainder will be the required converted number. Repeat Step 3 and Step 4, recording remainders from right to left, until the quotient becomes less than the digit of new base so that it cannot be divided.
Maths Formulas For NDA Exam Let’s have a quick revision of formulas that will help you in clearing the NDA 2023 and NDA 2024 exams and they are mentioned below in a topics wise manner: Mensuration 2. Geometry 3. Trigonometry 4. Heights and distances
Mathematical Formulas For NDA Exam: NDA Exam is just around the block and it must be giving nerves to many of you who want to clear it anyhow. But when it comes to mathematics, many of us have nightmares about it since it is not our strongest point. Maths gives us the chills and we make notes after notes and still aren’t able to score good marks and sometimes, not able to clear the cut-off. If you are going to attempt NDA Exam then the syllabus for the exam must be clear in your mind and the relevant details pertaining to it. NDA exam consists of general ability and maths and here, we will focus on maths exams.
The question paper of Maths is designed in such a manner that your abilities and skills related to the basic knowledge of formulas, calculation and accuracy with proper speed can be judged. 120 questions from the 300 marks for the maths question paper and the duration is very tightly packed of 150 minutes. First of all, you should know the important topics of maths and then shift your focus on the proper strategy and preparation tactics.
| TOPICS | MARKS | NO. OF QUESTIONS |
| TRIGONOMETRY | 50 | 20 |
| VECTOR ALGEBRA | 25 | 10 |
| ANALYTICAL GEOMETRY | 50 | 20 |
| PROBABILITY AND STATISTICS | 25 | 10 |
| ALGEBRA AND VECTOR ALGEBRA | 75 | 30 |
| INTEGRAL AND DIFFERENTIAL CALCULUS | 50 | 20 |
| TOTAL APPROX. | 300 | 120 |
In order to save your time and manage it accordingly, you should learn and use a variety of mathematical formulas and short tricks. This practice of saving time should be your primary concern as some questions are designed to have big calculations and they consume a lot of your time which may sabotage your plan later. Remember, the maths question paper may not look that hard because it is not but it is time-consuming for sure. So, get ready with the most valuable maths formulas and short tricks.
Maths Formulas For NDA Exam
Let’s have a quick revision of formulas that will help you in clearing the NDA 2023 and NDA 2024 exams and they are mentioned below in a topics wise manner:
- Mensuration

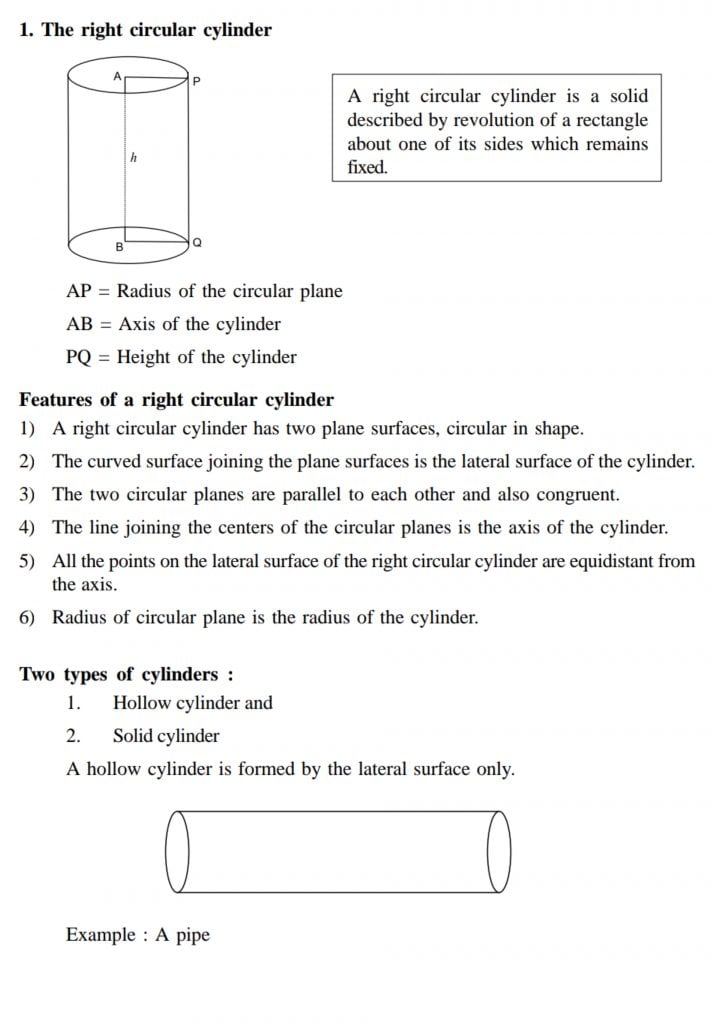
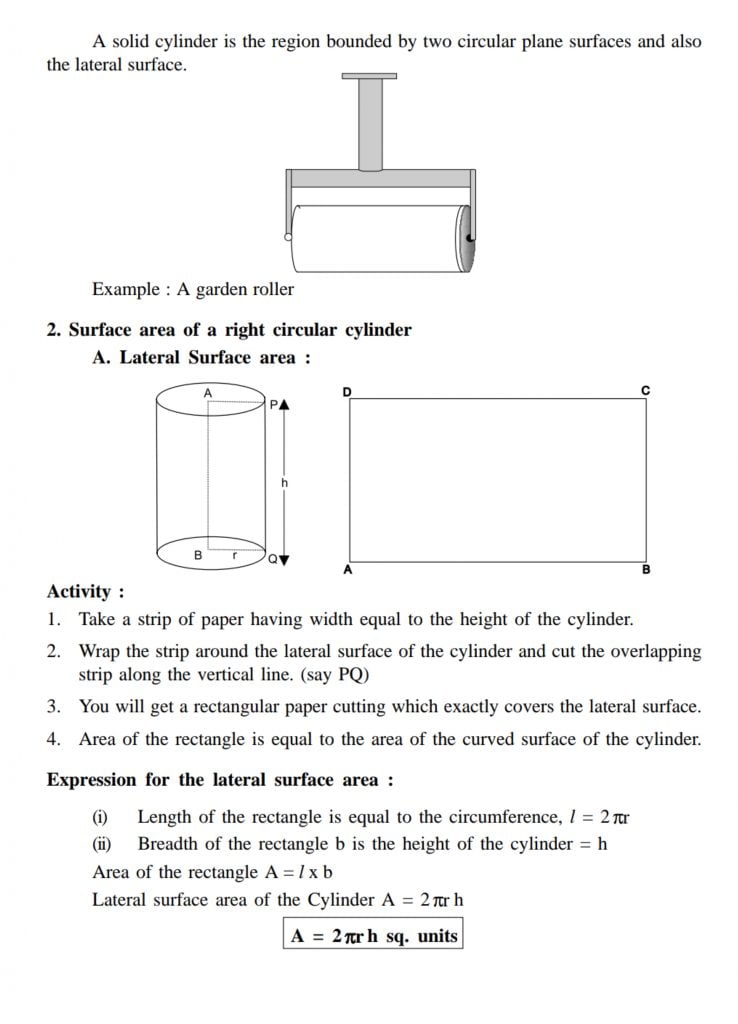
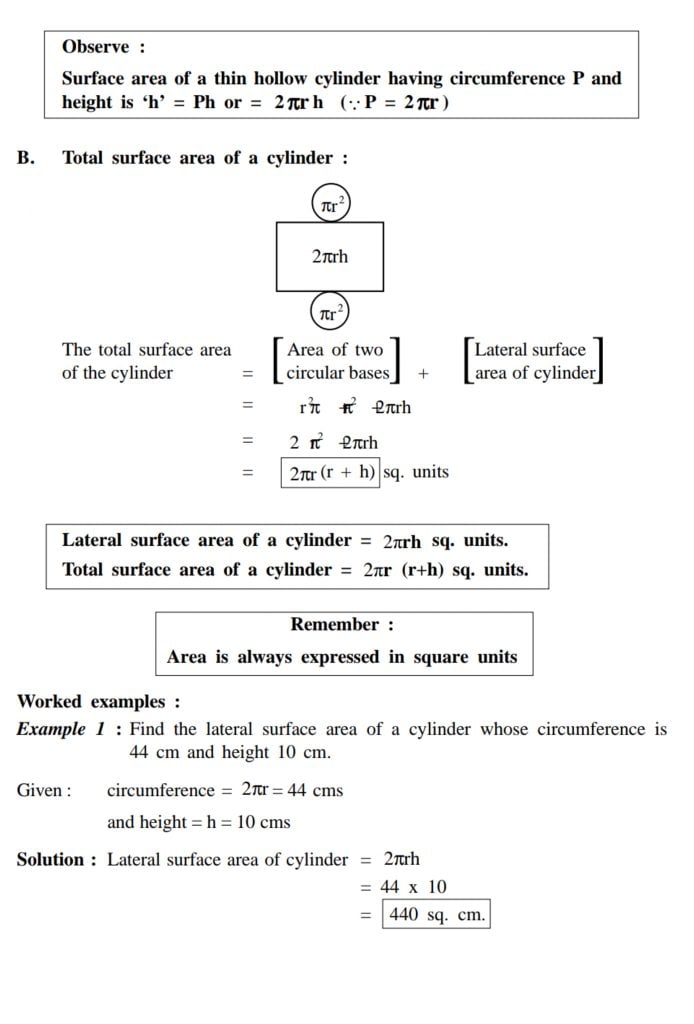
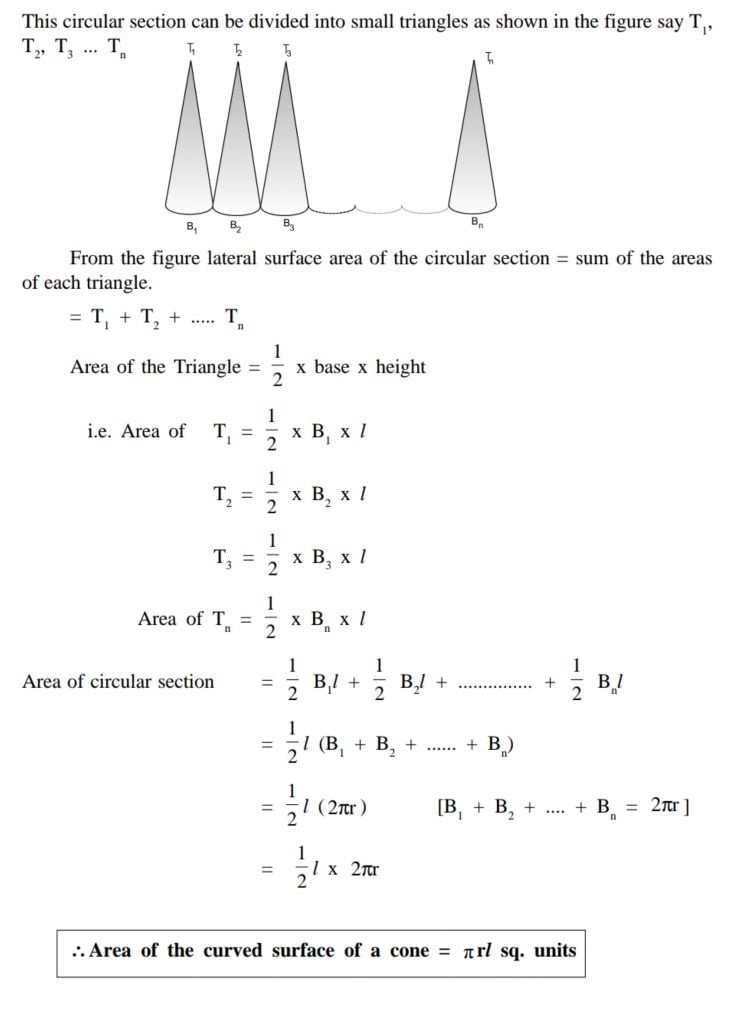
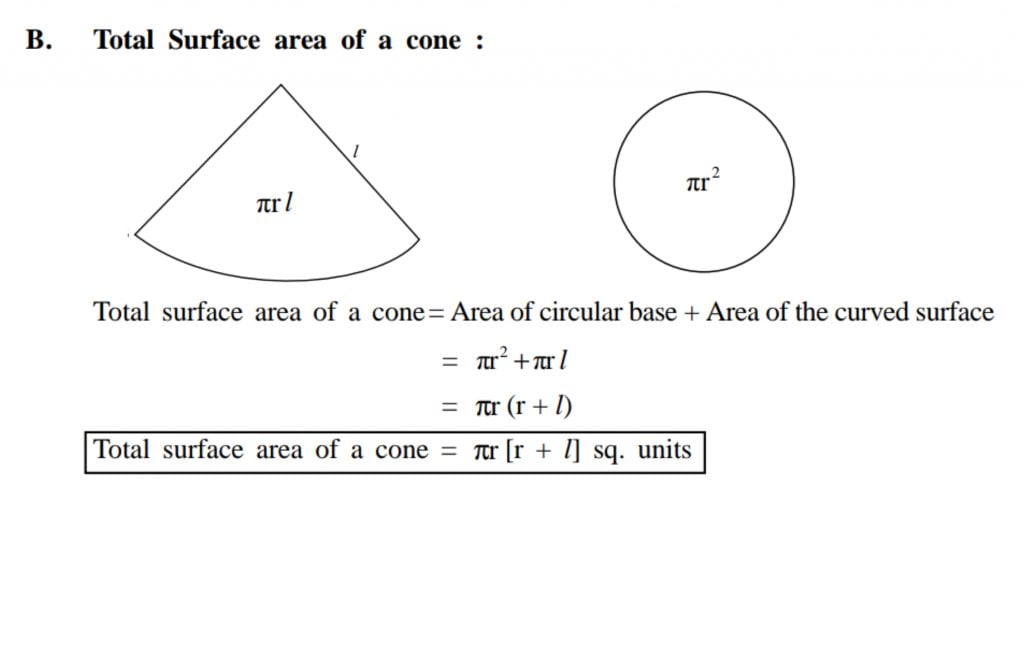




2. Geometry
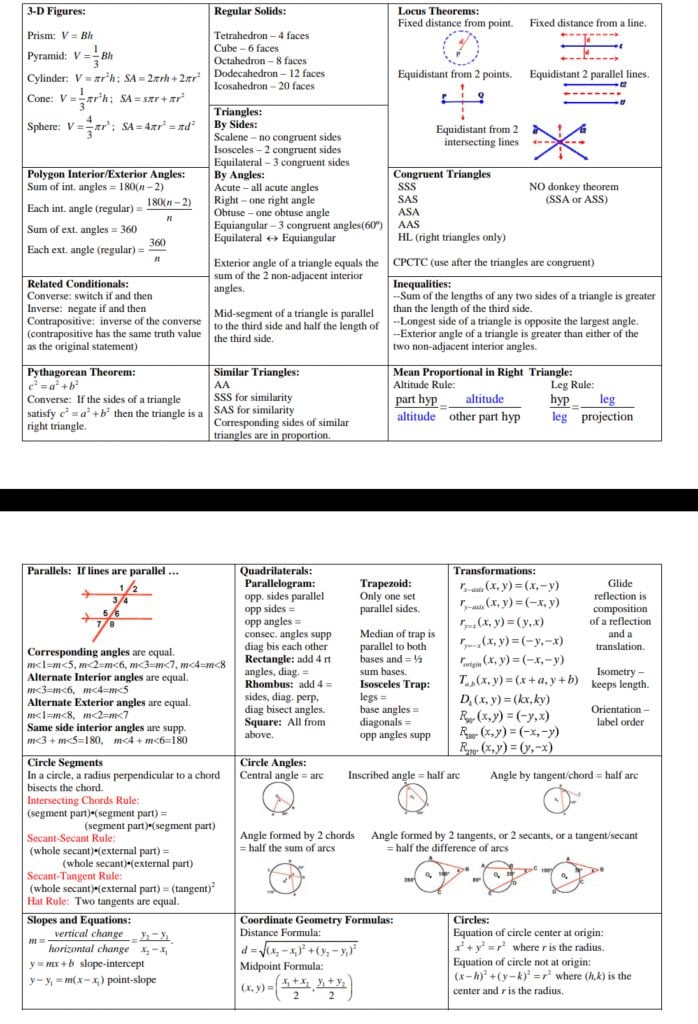
3. Trigonometry



4. Heights and distances


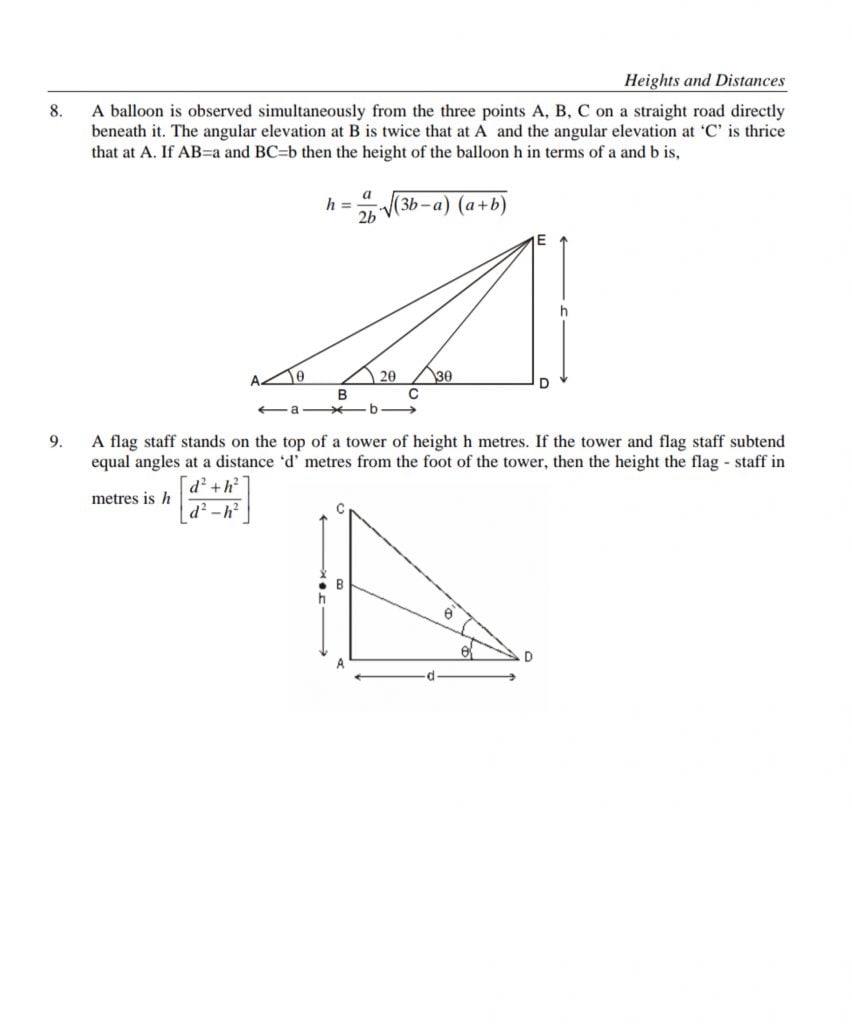
























1 thought on “100 Common Maths Formulas Used in NDA Exam”
It is quite useful for those who are preparing for prestigious NDA and CDS .
Thankyou so much sir