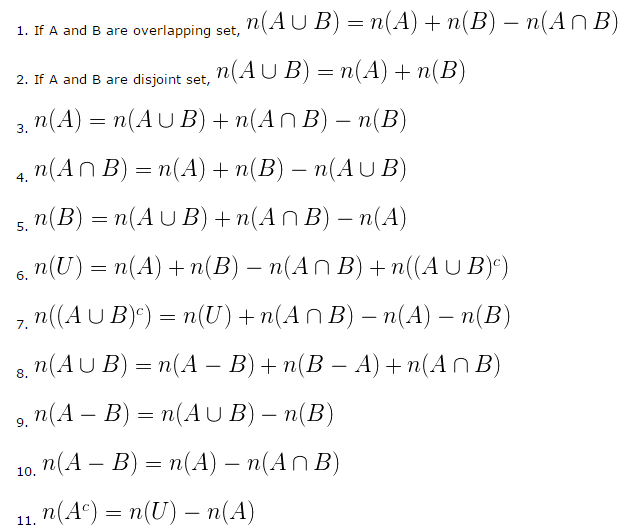NDA written exam is conducted by UPSC (Union Public Service Commission) twice every year. Candidates should know about the syllabus of the NDA written exam in the process of NDA exam preparation. In this article we will see NDA Exam important formulas and facts based on NDA exam mathematic syllabus topic name “Algebra”.
Prepare for NDA Exam Online
NDA Paper 1 Mathematics syllabus:
- Algebra
Concept of a set, operations on sets, Venn diagrams, De Morgan laws, Cartesian product, relation, equivalence relation, Representation of real numbers on a line, Complex numbers – basic properties, modulus, argument, cube roots of unity, Binary system of numbers, Conversion of a number in decimal system to binary system and vice-versa, Arithmetic, Geometric and Harmonic progressions. Quadratic equations with real coefficients, Solution of linear inequations of two variables by graphs, Permutation and Combination, Binomial theorem and its applications, Logarithms and their applications.
- Matrices and Determinants
- Trigonometry
- Analytical Geometry – 2D and 3D
- Differential Calculus
- Integral calculus and Differential equations
- Vector algebra
- Statistics and Probability
NDA Exam important formulas set 1 Algebra
- Set Theory is a branch of mathematics which deals with the study of sets or the collection of similar objects.
- Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both. The union of{1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4} .
- Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B. The intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3} .
- Set difference of U and A, denoted U \ A, is the set of all members of U that are not members of A. The set difference{1,2,3} \ {2,3,4} is {1} , while, conversely, the set difference {2,3,4} \ {1,2,3} is {4} . When A is a subset of U, the set difference U \ A is also called the complement of A in U. In this case, if the choice of U is clear from the context, the notation Ac is sometimes used instead of U \ A, particularly if U is a universal set as in the study of Venn diagrams.
- Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1,2,3} and {2,3,4} , the symmetric difference set is {1,4} . It is the set difference of the union and the intersection, (A ∪ B) \ (A ∩ B) or(A \ B) ∪ (B \ A).
- Cartesian product of A and B, denoted A × B, is the set whose members are all possible ordered pairs (a,b) where ais a member of A and b is a member of B. The cartesian product of{1, 2} and {red, white} is {(1, red), (1, white), (2, red), (2, white)}.
- Power set of a set A is the set whose members are all possible subsets of A. For example, the power set of {1, 2} is{ {}, {1}, {2}, {1,2} } .
- Set Theory Formulas (Notations):

- For a group of two sets: